
Что такое индукция и напряженность магнитного поля
Удобная навигация, видео-разборы тем, задачи для самопроверки — всё это в вашем кармане. А ещё раздел с полезными материалами, календарь занятий и уведомления о предстоящих уроках. Силовой характеристикой магнитного поля в каждой его точке является векторная величина , называемая вектором магнитной индукции поля. За направление вектора магнитной индукции принимается то, в котором устанавливается свободная воображаемая магнитная стрелка, или нормаль к витку с током. За направление вектора магнитной индукции принимают направление, на которое указывает северный полюс свободно вращающейся магнитной стрелки, помещённой в данное поле.


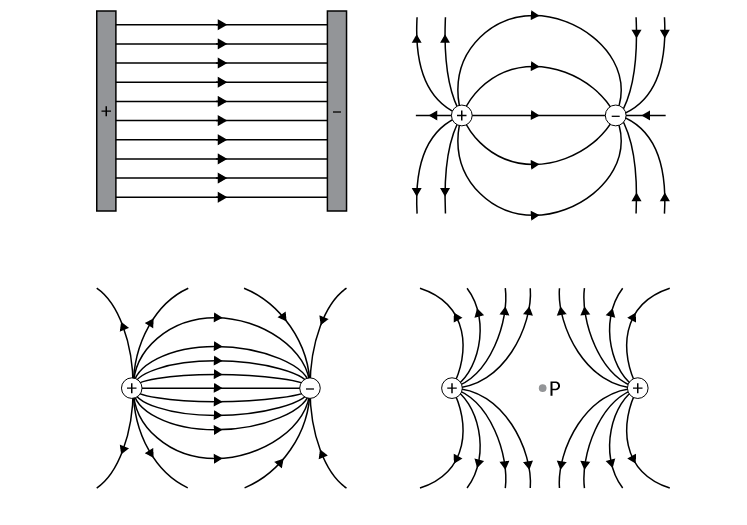




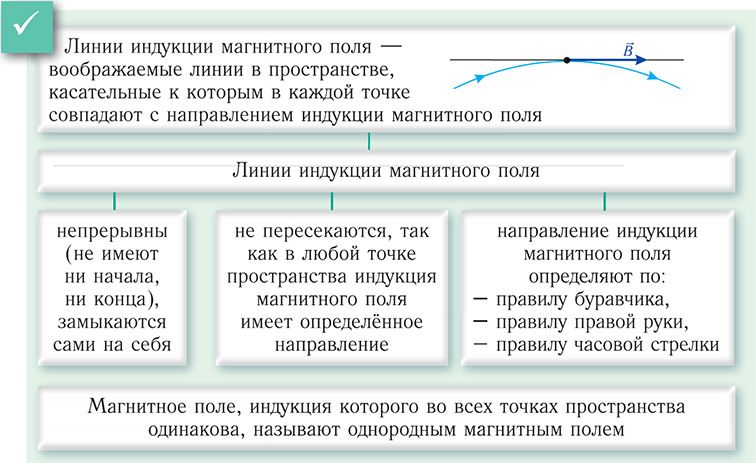



Эти величины связаны между собой. Рассмотрим, что такое напряженность магнитного поля, чему она равна, каков физический смысл этой величины. Единица измерения напряженности магнитного поля в системе СИ - ампер на метр А м п е р м е т р. Индукция магнитного поля - силовая характеристика.
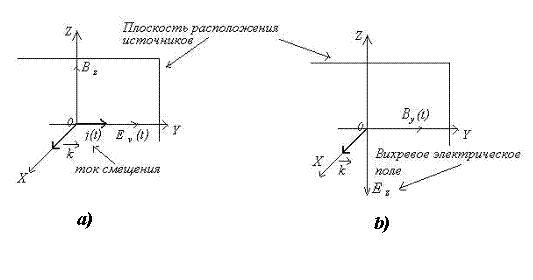






Тензор электромагнитного поля Тензор энергии-импульса 4-потенциал 4-ток. Вместе с выражением для силы Лоренца , задающим меру воздействия электромагнитного поля на заряженные частицы, эти уравнения образуют полную систему уравнений классической электродинамики , называемую иногда уравнениями Максвелла — Лоренца. Уравнения, сформулированные Джеймсом Клерком Максвеллом на основе накопленных к середине XIX века экспериментальных результатов, сыграли ключевую роль в развитии представлений теоретической физики и оказали сильное, зачастую решающее влияние не только на все области физики, непосредственно связанные с электромагнетизмом , но и на многие возникшие впоследствии фундаментальные теории, предмет которых не сводился к электромагнетизму одним из ярчайших примеров здесь может служить специальная теория относительности. Жирным шрифтом в дальнейшем обозначаются векторные и псевдовекторные величины, курсивом — скалярные. Приведённые выше уравнения Максвелла не составляют ещё полной системы уравнений электромагнитного поля , поскольку они не содержат свойств среды, в которой возбуждено электромагнитное поле. При помощи формулы Остроградского — Гаусса и теоремы Стокса дифференциальным уравнениям Максвелла можно придать форму интегральных уравнений :.




Похожие статьи
- Сшить плащ своими руками выкройки - Выкройка юбки-полусолнце Как сшить юбку-полусолнце своими руками
- Если не получается забеременеть второй раз что делать
- Системы автополив своими рукам - Как отремонтировать наушники дома? Подробная инструкция
- Как сделать тёплый пол в деревянном доме своими руками - Теплый пол в деревянном доме - виды и спосо