Урок "Углы между касательной к окружности и хордой, проведенной в точку касания" (9 класс)
ЕГЭ по математике — обязательный предмет. Однако выпускники могут выбрать, на каком уровне сдавать ЕГЭ по математике: базовом или профильном. Результатов базового ЕГЭ будет достаточно для получения школьного аттестата, а результаты «профиля» могут пригодиться при поступлении в вузы. При этом минимальные баллы за ЕГЭ разных уровней отличаются. Поиск по сайту. Выбираем образование Юридическое образование Как стать успешным юристом Профессия экономист Экономика и финансы IT-технологии и телекоммуникации Программирование Профессия психолог Религиозное образование Культурное образование Медицинское и фармацевтическое образование.
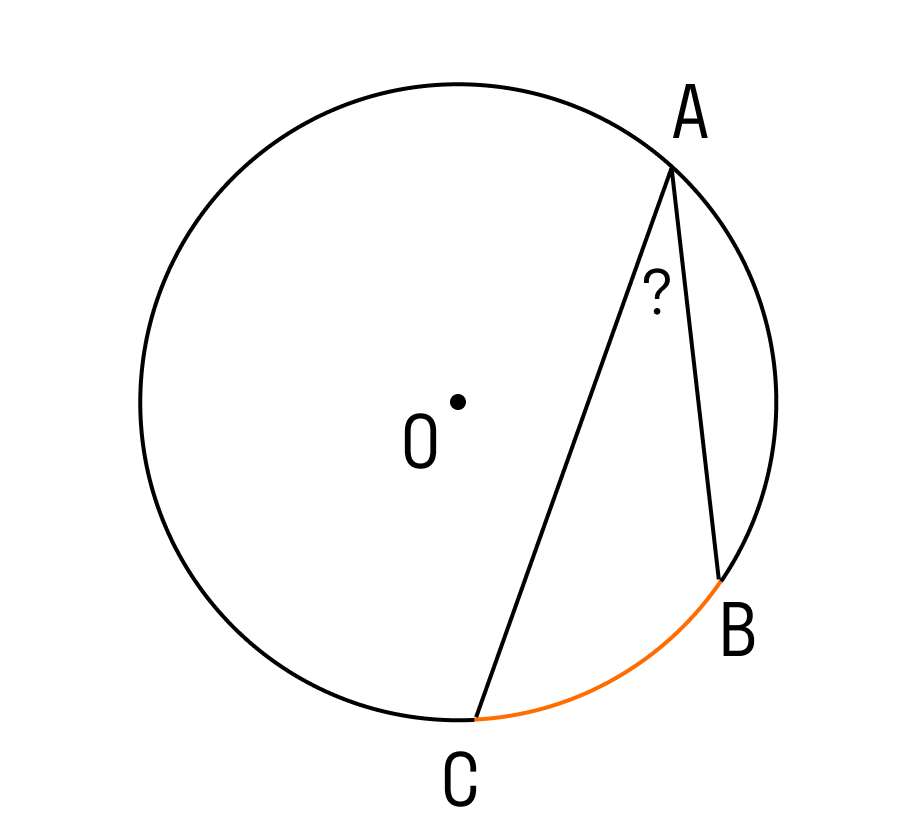



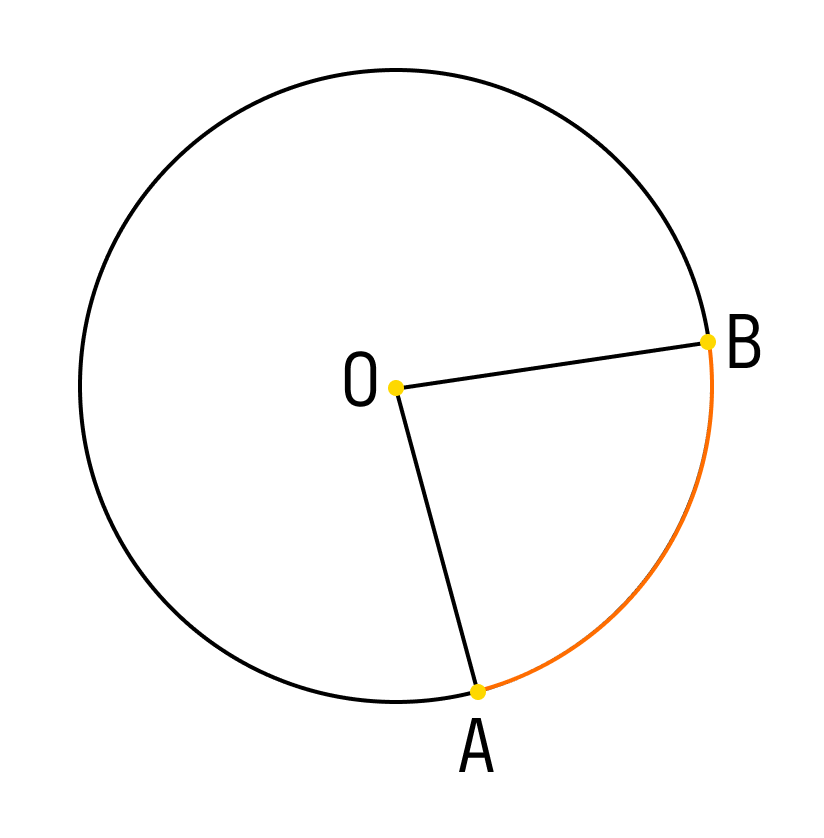


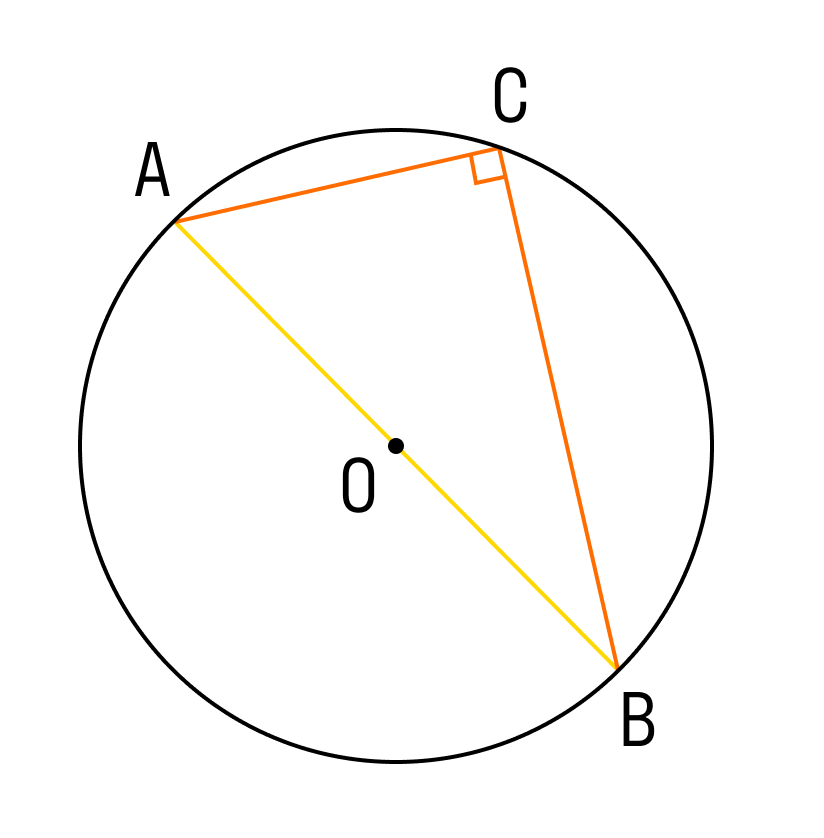

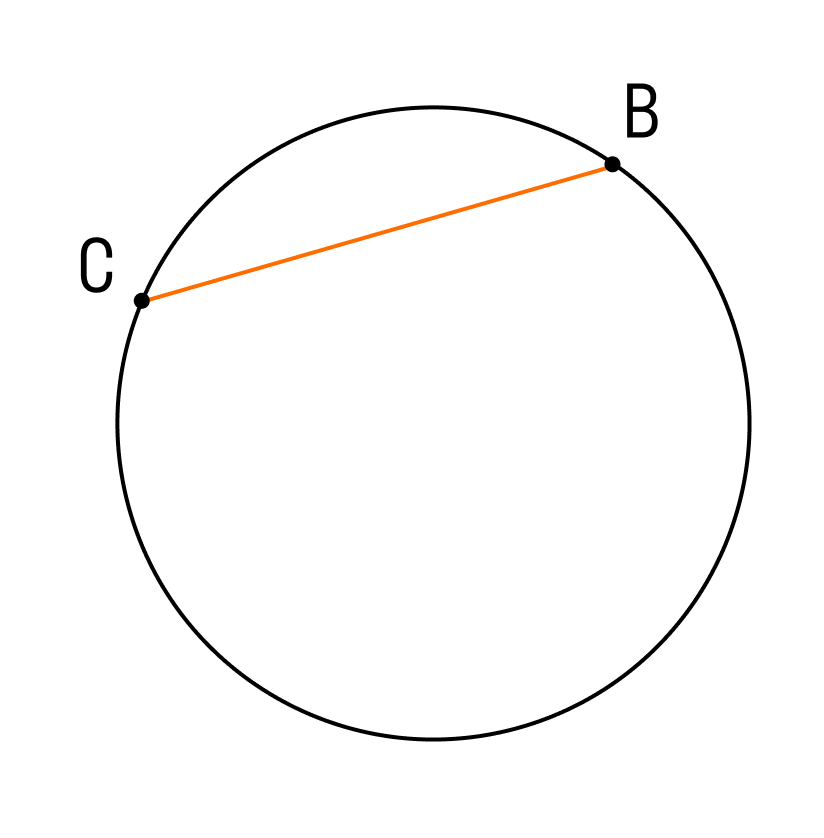
Вход Регистрация. Учебные заведения. Проверочные работы. Поиск по сайту. Если на окружности отметить две точки, они разделят окружность на две дуги.
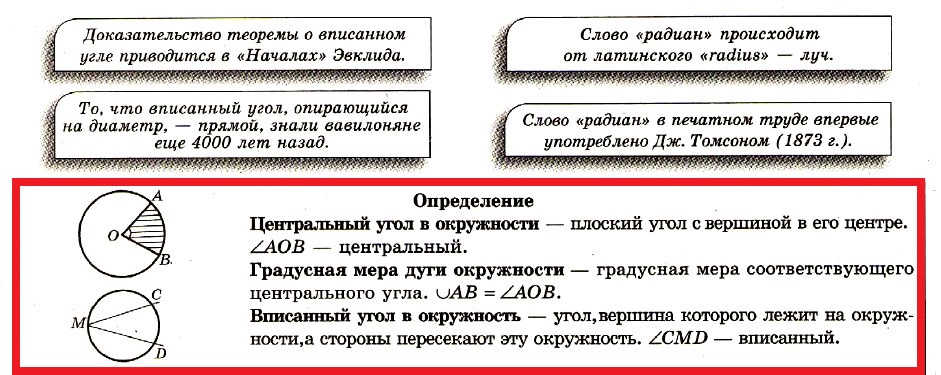
- Центральные и вписанные углы.
- В этом параграфе рассматриваются неравенства, содержащие переменную под знаком абсолютной величины под знаком модуля. Во многих случаях для решения таких неравенств целесообразно разбить числовую ось на промежутки так, чтобы функции, стоящие под знаком модуля, на каждом из промежутков сохраняли знак, т.
- Темы исследовательских работ по истории математики. История математики.
- Слушателям, успешно освоившим программу, выдаются удостоверения установленного образца.
- Технологическая каота соответствует требованиям ФГОС. Урок имеет практическую направленность на успешную сдачу ОГЭ.
- Математика в школе.
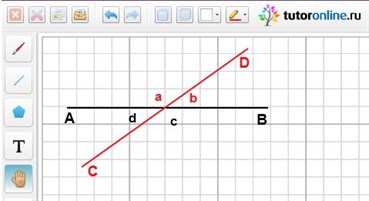



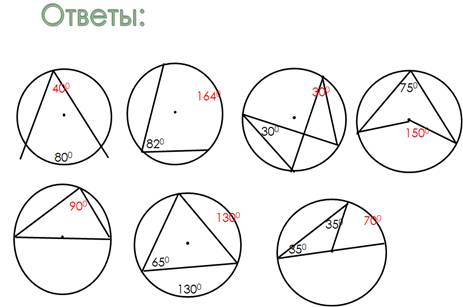





Задача на вписанную или описанную окружность. Найти угол Д. В одном видео можно было увидеть, как преподавателям на каком-то семинаре опытный преподаватель показывал, около какой окружности можно описать окружность. Преподаватель, даже не рисовал эту окружность, а просто ловко решал, что вокруг этого четырёхугольника окружность легко описать, а вокруг другого - нельзя. Материал не сложный, но его не всегда рассматривают для каждого учащегося 6 - 9 классов.