Раскраска графов
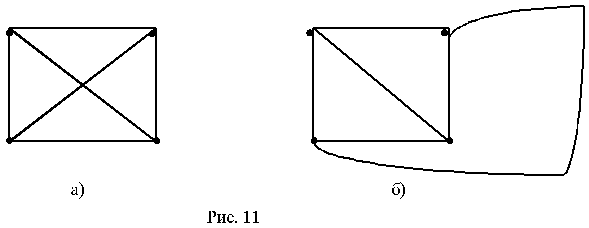
Так как граф является двудольным тогда и только тогда, когда все циклы четны, определить двудольность можно за один проход в глубину. На каждом шаге обхода в глубину помечаем вершину. Произведём серию поисков в ширину. Ту вершину, из которой мы начинаем идти, мы помещаем в первую долю. В процессе поиска в ширину, если мы идём в какую-то новую вершину, то мы помещаем её в долю, отличную от доли текущей вершину.

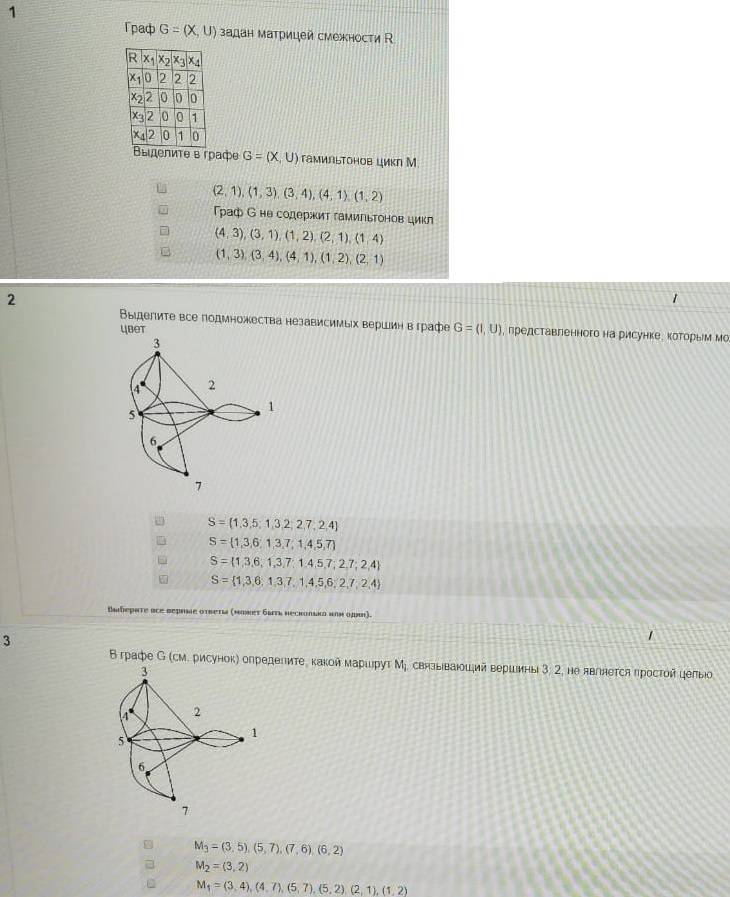









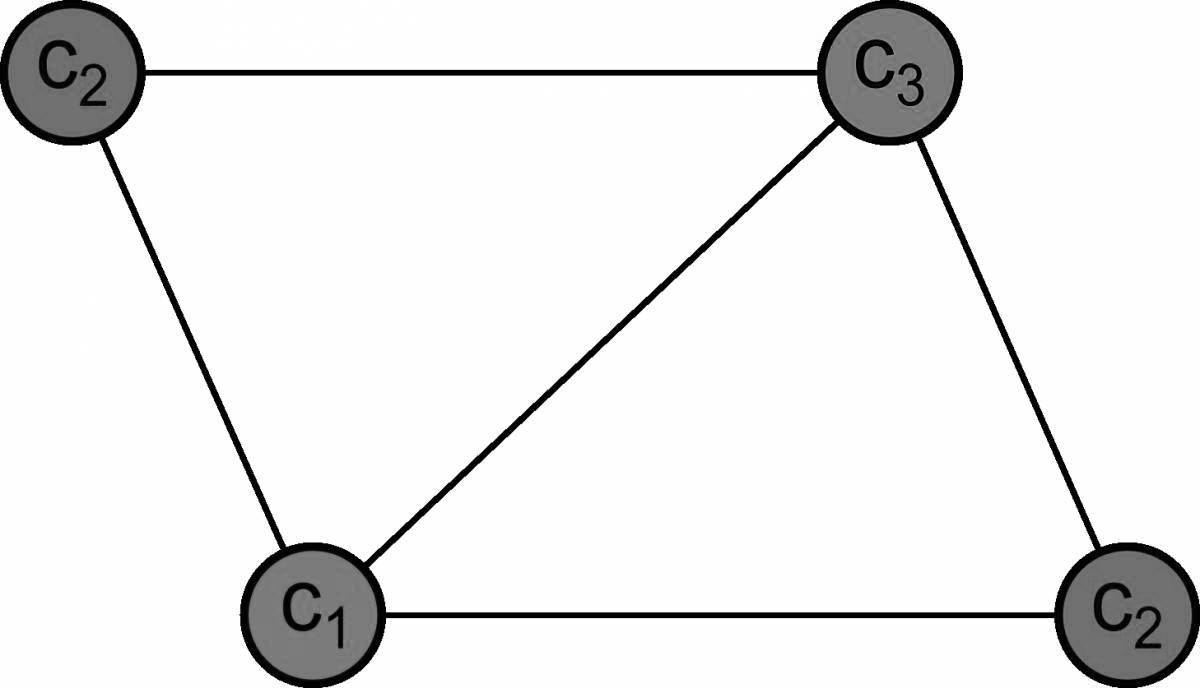
Раскраской графа G в k цветов или k -раскраской называется разбиение элементов графа на k классов. Раскраска называется правильной , если никакие две смежные вершины не получают одинаковый цвет то есть смежным вершинам приписываются различные натуральные числа. Граф, для которого существует правильная k -раскраска, называется k -раскрашиваемым.
- При решении практических задач с применением графов возникает необходимость в разбиении множества вершин графа на классы попарно несмежных между вершин. Довольно часто дополнительно требуется, чтобы таких классов было наименьшее число.
- Работа выполнена на кафедре высшей математики факультета прикладной матсматики-процессов управления Санкт-Петербургского государственного университета.
- Первоначально раскраски графов были нужны для составления географических карт [1].
- Категория: Математика.
- Заметим, что рассуждение теоремы Форда — Фалкерсона фактически является алгоритмом нахождения максимального потока между двумя вершинами или доказательством того, что этот поток является максимальным.
- Актуальность теш. Согласно теореме Штейница г.
- При решении практических задач с применением графов возникает необходимость в разбиении множества вершин графа на классы попарно несмежных между вершин.
- Раскрашивать можно как ребра графа, так и вершины. Коснемся сначала задачи о раскраске вершин,.
- Раскраска графа - это процесс присвоения цветов вершинам графа таким образом, чтобы никакие две смежные вершины не имели одинаковый цвет.

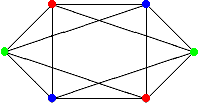


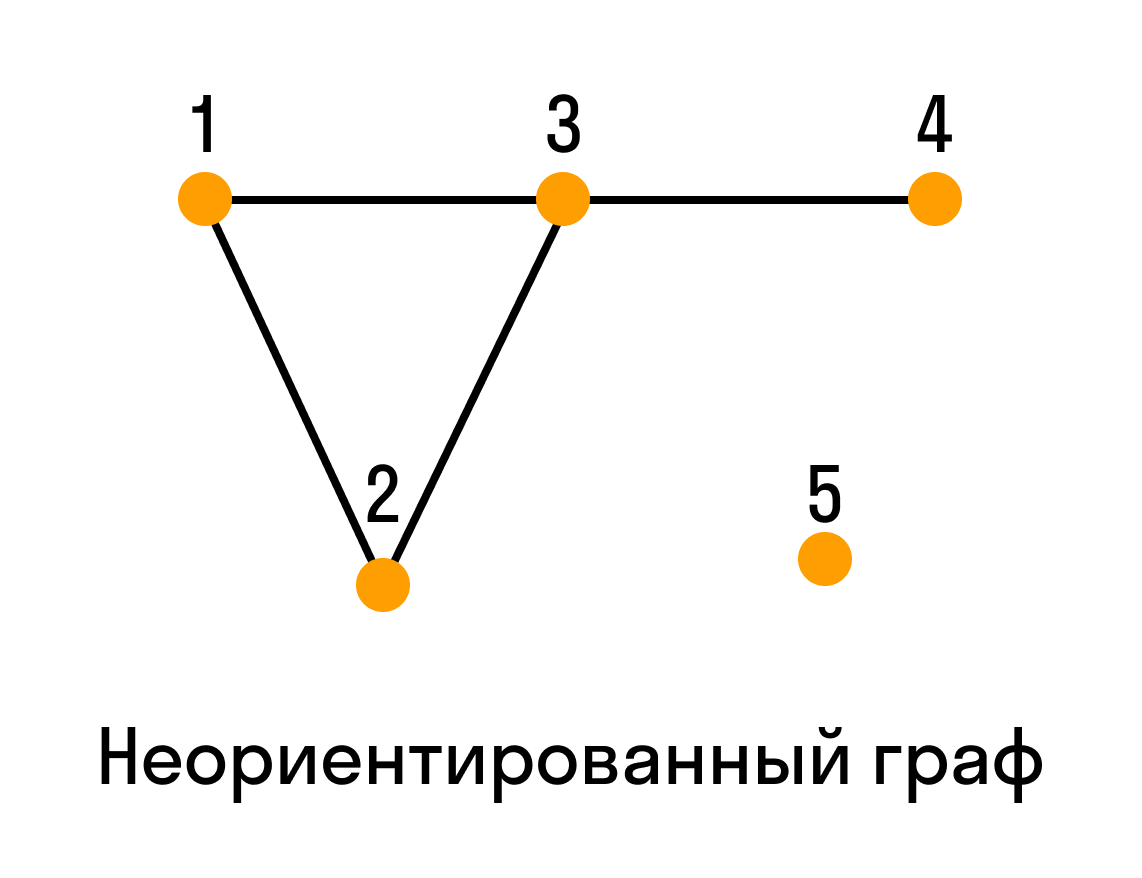
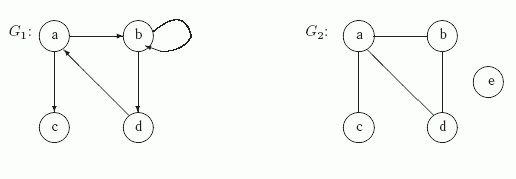
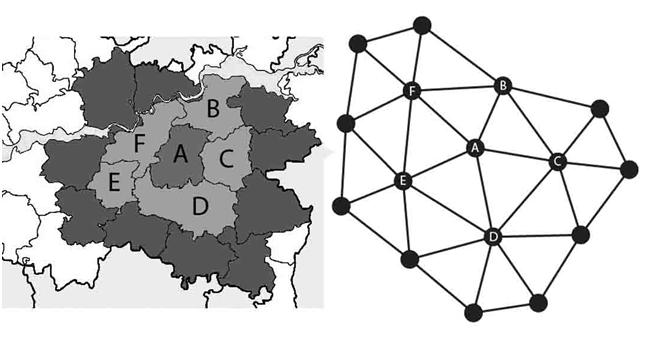

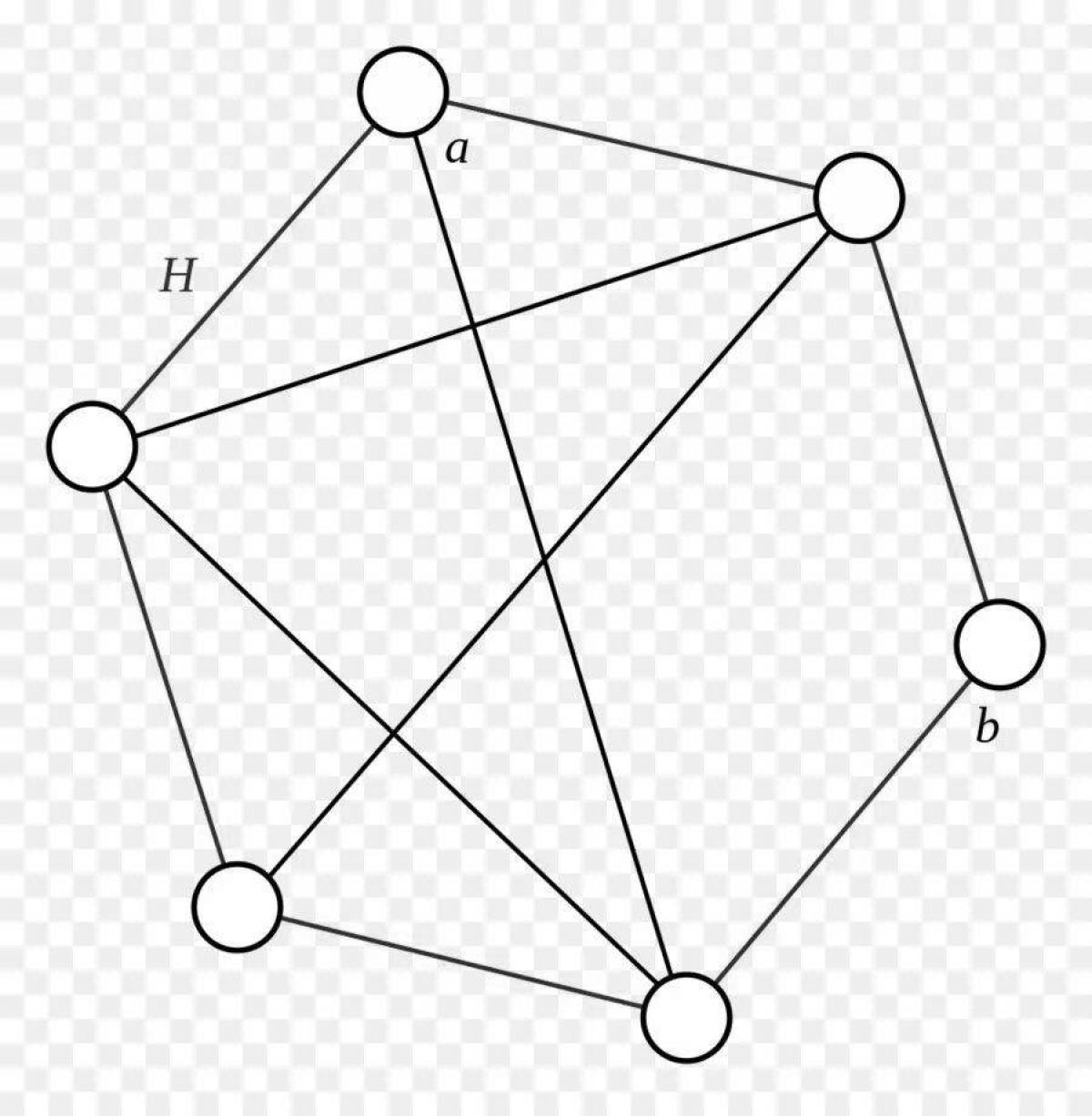



Раскраска графа — это процедура присвоения цветов каждой вершине графа G таким образом, что смежные вершины не получают одинаковый цвет. Цель состоит в том, чтобы минимизировать количество цветов при окрашивании графика. Наименьшее количество цветов, необходимое для окраски графа G, называется его хроматическим числом этого графа.